L'Hokuyo c'est cool, mais l'Hokuyo c'est quoi ?
L'Hokuyo est un télémètre laser, un LiDar. Il faut imaginer un capteur qui crée une “nappe laser” autour de lui et qui renvoit la position des objets dans ce plan. Plus précisément, nous possédons un modèle URG-04LX-UG01 de la marque Hokuyo (d'ou le nom). Vous pouvez trouver les caractéristiques techniques ici : http://www.hokuyo-aut.jp/02sensor/07scanner/urg_04lx_ug01.html

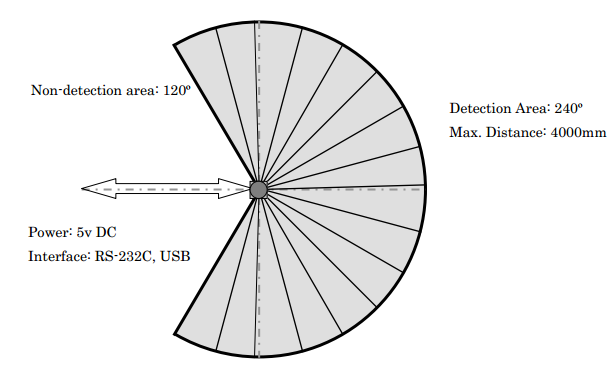Comme je l'ai expliqué plus haut, un télémètre laser balaye un plan à l'aide d'un laser rotatif, créant une “nappe laser”. Tout objet dans ce plan va renvoyer le laser et permettre au télémètre d'en connaitre la distance. Notre Hokuyo par exemple, balaye sur 240° avec une résolution de 1024 points par tour, soit environ 700 points sur 240°.
On se doit d'évoquer deux points problématiques de ces télémètres (ils sont magiques, mais pas trop) :

1. Un télémètre laser n'est pas TRES précis. J'entend par la que la précision est de quelques centimètres (plus ou moins 3% pour notre hokuyo - soit plus ou moins 9cm à 3 mètres). Certes en pratique les télémètres s'avèrent bien plus précis que ces valeurs extrèmes quand ils sont utilisés dans des conditions optimales mais cette précision reste tout de même de l'ordre du centimètre. C'est plus que suffisant pour détecter les adversaires mais pas assez pour remplacer l'odométrie.
2. Un télémètre possèdes des angles morts. En effet comme disait Coluche “un train peut en cacher un autre” (quoi ya pas que lui qui le dit ?). Avec un seul hokuyo, si un robot se trouve juste devant la balise, un va masquer tout le reste de la carte et nous deviendrons alors aveugles. Le problème peut être résolu par l'ajout d'un deuxième hokuyo.

Parlons de l'Hokuyo en particulier, et plus précisémment de notre modèle. Comment communique-t-on avec lui et sous quelle forme ?
L'hokuyo est relié à un ordinateur par cable USB. Il va créer une interface serial dans les périphériques (/dev/ttyACMx). Nous communiquons avec l'hokuyo à l'aide d'une librairie C : v0.8.18. Nous avons utilisé la version 1.0.4 auparavant mais elle beugue avec deux Hokuyo.
Toute la documentation est disponible sur le site. La documentation est plutôt faible et incomplète. Je vais donc essayer de fournir les informations essentielles à l'utilisation de l'hokuyo et les quelques pièges dans lesquels il ne faut pas tomber.

Utilisation :
L'hokuyo renvoit simplement un tableau de long. Cela correspond à la distance des points. Nous avons donc des distance associées à des index. Il est facile de transformer index en angle à l'aide d'une fonction présente dans la librairie. On peut donc conclure que l'hokuyo nous renvoit des coordonnées radiales. Un simple cosinus/sinus les transformera en coordonnées cartésiennes. Je ne m'étend pas sur le sujet, les exemples de la documentation sont facile à comprendre.

Voici une liste de ce que l'on peut faire :

• Récupérer un tableau de mesure
• Demander à l'hokuyo de mesurer en continu ou juste un certain nombre de fois.
• Demander à l'hokuyo de “sauter” des mesures
• Définir le champ de mesure en angle
• Définir un champ de mesure en distance (attention, c'est en radial)

Petits pièges :

• L'hokuyo scane dans un plan, certes, mais en réalité c'est un ensemble de points, à grande distance, l'écart entre deux points n'est pas négligeable (plusieurs centimètres !), il faut donc en tenir compte dans les algos de filtrage et de reconnaissance de robot.

• Il ne sert à rien de chercher à récupérer les informations d'intensité et de multi-echo, bien que présent dans la librairie, le matériel ne le permet pas.

Clarification de la doc :
Angle, Index, Step : Il existe trois manière de représenter l'angle d'une mesure : son angle (ce que l'on utilise), son index (son numero de mesure) et sa step (son angle en représentation interne). Petit détail au passage : 0° est le point “en face” de l'hokuyo.
En pratique voila ce qu'il faut retenir :
Nous utilisons l'angle, on peut le récupérer à l'aide d'une fonction type index_to_angle.
L'index est, comme son nom l'indique, l'index de point dans le tableau de retour.
Si le domaine de mesure ne change pas, l'angle asocié à un index reste le même
Les steps sont la représentation interne de l'angle, cela ne nous intéresse pas et n'est pas utilisable pour nous. On les utilise uniquement pour définir le domaine de mesures. On se sert alors d'une fonction du type angle_to_index.

Données max :
Un point bien angigu qui m'a vallu de bonnes prises de tête. Une fonction est disponibles pour connaitre le nombre maximal de points que renverra l'hokuyo. Cette fonction renvoit une donnée liée au matériel et non à la configuation de celui-ci.
Ce qu'il faut comprendre est :
Si j'utilise l'hokuyo “par défaut”, que je demande le nombre max de mesure, l'hokuyo me répondra par exemple 700. Je vais récupérer les données, je récupère 700 données.
Si je paramètre l'hokuyo pour effectuer des mesures sur uniquement 120° (au lieu de 240) et que le lui demande le nombre max de mesure, il répondra AUSSI 700 mais lorsque je demande les données, je n'en recoit que 350.
Ainsi si vous souhaitez connaitre le VRAI nombre de données que renvoit l'hokuyo, il faut faire une mesure, et l'hokuyo renverra le nombre de données qu'il a envoyé. Si le domaine de mesure ne change pas, le nombre de données renvoyées ne changera pas non plus.

Multi-echo / Intensité :
Je me répète ici, mais inutile de chercher à récupérer les données de multi-echo et d'intensité. Bien que les fonction existent, le matériel ne le supporte pas.

Quelques précision sur des points importants liés au matériel :

Bien que la consommation de l'hokuyo soit de 2.5W, il est nécessaire d'utiliser le cable double, ou une alimentation externe. En effet il semblerait que 0.5A ne suffient pas au bon fonctionnement de l'Hokuyo. Si une alimentation externe est utilisée, attention tout de même aux raccordement, l'expérience m'a appris que si vous branchez cela n'importe comment, les données seront corrompues et il sera impossible d'utiliser l'hokuyo !

L'hokuyo scanne dans un plan, il est donc important que celui-ci soit bien droit lors des matchs. S'il est de travers, la précision sera moins bonne, et on risque même de ne plus détecter les robots !

L'hokuyo renvoit une liste d'entiers, chacun étant la distance de l'echo à un certain angle. Il faut alors traiter ces données. La première étape est de grouper ces points en cluster.

Voici l'algo utilisé :

tab[] tableau des distance
culsters[] tableau des clusters
nb_clusters = 0
found_cluster = false

Pour i de 0 à size(tab):
  found_cluster = false
  Pour j de i-1 à max(0, i - search_size): //parcours inverse
    Si distance(tab[i], tab[j]) < distance_max:
      clusters[i] = clusters[j]
      found_cluster = true
      break
      
  Si found_cluster == false :
    clusters[i] = nb_clusters
    nb_cluster += 1
    

On note les variables de réglage search_size et distance_max :

• search_size est un entier désignant le nombre points précédents parmis lesquels chercher un cluster existant
• distance_max désigne la distance en dessous de laquelle un point est rattaché à un cluster existant

Cet algorithme se base sur le fait que les liste renvoyées par l'hokuyo sont triées par angle.

Suite à cela, on dispose de groupes (clusters) de points. Le groupe point étant stocké dans le tableau cluster[]. On peut alors filtrer les groupes ne comporte qu'un faible nombre de points, qui ont de fortes chances d'être des parasites.

Il faut ensuite convertir les coordonnées du repère polaire au repère cartésien. Chaque index correspond à un angle, que l'on peut récupérer par une fonction de la librairie. Selon la manière dont seront traités les points et les groupes, il peut être intéressant de précalculer les sinus/cosinus en fonction de l'angle. En effet, a chaque scan de l'hokuyo, un même index correspondra toujours au même angle. Ainsi il suffir d'initialiser l'hokuyo puis de calculer les tableaux d'équivalence index↔sin et index↔cosinus.

Il suffira alors pour convertir les points dans le repère cartésien d'effectuer :

x[i] = tab[i]*sin_tab[i]
y[i] = tab[i]*cos_tab[i]

au lieu d'appeller pour chaque point, à chaque scan, les fonction sinus et cosinus.

Dans l'absolu, l'hokuyo devrait renvoyer un nombre de cluster égal au nombre de robots sur la carte. Or il peut arriver que l'on détecte un objet en trop (un arbitre qui passerait sa main au dessus de l'aire de jeu par exemple). On se propose donc de filtrer les cluster de la manière suivante :

Calculer la taille de chaque cluster (en millimètres, pas en nombre de points)
Trier les cluster par taille décroissante
Garder les X premiers (X étant le nombre de robots attendus)

Un autre avantage de ce tri est qu'il peut permettrede différencier les deux robots adverses en fonction de la taille de la balise. Par exemple, on peut mettre une balise plus petite sur le petit robot adverse afin de le reconnaitre. Le gros robot sera donc toujours avant le petit dans la liste des robots détectés.